Surface tension
The surface tension in soap bubbles is increased by the water and decreased by the soap

We can think of a soap bubble as air surrounded by water and soap. The air trapped inside will add a pressure to the soap film from the inside, and the air surrounding the bubble will add a pressure to the soap film from the outside. This means that the soap film feels a pressure from two sides; the inside and the outside. The air pressure inside the bubble will always be larger than the air pressure from the outside.
One could ask: Why does the bubble not grow over time, if the pressure inside is larger than the pressure outside? We have to take another pressure into account: The pressure from the soap film itself, towards the centre of the bubble. As a result of surface tension the soap film will minimize its surface area by making the bubble as small as possible. Hence the bubble does not grow because there is a balance between the pressure inside the bubble and the pressure from the soap film plus the air pressure from the outside.
The bigger the bubble, the lower the pressure! The pressure in an infinitely small bubble will, in principle, be infinitely large. Therefore there are limit to how small a bubble that can be produced. The pressure difference between two bubbles becomes apparent, if they are produced at a flat surface touching each other, so that they have a shared soap film. The pressure difference in two equally sized bubbles must be zero, and the shared soap film will be flat. If the bubbles have different sizes, and therefore different air pressures, this will be seen as the shared soap film will bulge out from the one with the highest pressure. If you make the experiment, you will actually see that the small bubble is bulging out into the big one. This illustrates that the pressure in small bubbles is bigger than in larger bubbles.

Two bubbles of the same size has the same air pressure and therefore there is a straight soap film between the two bubbles

A small bubbles has higher air pressure and therefore the soap film bulges into the big bubble
En lille boble har et større tryk og derfor buler sæbehinden imellem dem ind i den store boble
The air pressure of two equally sized bubbles is the same. Thiscan be seen from the flat shared soap film between the two equally sized bubbles If the bubbles have different sizes the shared soap film will bulge from the small bubble into the larger. This shows us that the air pressure in small bubbles is higher than the air pressure in larger bubbles.
The air pressure, p inside a soap bubble can be described mathematically as,
[latex] p = \frac{ 4 \sigma }{ r } [/latex]
where [latex] \sigma [/latex] is the surface tension of the liquid and r is the bubble radius. The equation is based on the famous Laplace-Young equation which was discovered in 1806 by Marquis de Laplace:
[latex] \Delta p = \sigma ( \frac{ 1 }{ R1 } + \frac{ 1 }{ R2 } ) [/latex]
The Laplace-Young equation describes the pressure difference across a surface which acts as a border for liquids or gasses. Every point on such a surface has two characteristic curvatures: a maximal and a minimal curvature. These will always be normal (perpendicular) to each other. In the equation the curvature is expressed as a radius (R1 or R2) of the circle that can be fitted to the surface.

The excess pressure inside a soap bubble is related to the size of the bubble, as can be seen from the graph.
The pressure is higher in smaller bubbles than in larger ones.

The maximal and minimal curvature in a point at the surface of an egg. The curvatures will always be normal (perpendicular) to each other
A soap film with no air trapped inside it is a so-called minimal surface. The air pressure on each side of the film will be the same, and from the Laplace-Young equation we can see that the total curvature in a given point is zero:
[latex] 0 = \Delta p = \sigma ( \frac{ 1 }{ R1 } + \frac{ 1 }{ R2 } ) = \frac{ 1 }{ R1 } + \frac{ 1 }{ R2 }[/latex]
This means that for every point on a minimal surface, the maximal and minimal curvature will be equal in size and in opposite directions. This is of course true when the curvature in both directions is zero, as it is for a flat surface. It is more surprising that it is true for more complex minimal surfaces such as a catenoid.

The surface tension in soap bubbles is increased by the water and decreased by the soap
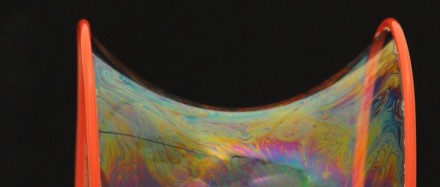
Read about and look at the fascinating shapes of soap bubbles

The best recipes for mixtures for small and large soap bubbles that last longer