The color of soap bubbles
Where does the color of the bubbles come from?
A free floating soap bubble is for example always spherical and a soap film in a flat bubble wand is always flat. The area of the soap film is in both cases minimal.
A free floating soap bubble will always be spherical because the bubble minimizes it surface area.
A soap film in a wand is always flat because soap films minimized their surface area.
In the mathematical world it is true that a bubble is perfectly spherical or the film in the wand is perfectly flat. In our physical world however, gravity will also play an important role for the shapes of the soap film disturbing their perfect shapes. In this text we will apply the mathematical perspective and forget about gravity.
Minimal constructions are what we call structures that minimize their surface areas. What characterizes a minimal construction is that its surface area is minimized given some specific constraints. The constraints could for example be the shape of the bubble wand or it could be the volume of air trapped inside the soap film. Gravity could also be such a constraint. The soap film cannot change the initial constraints, but it can change its surface shape.
If a soap film does not contain any bubbles, it can be called a minimal surface. A minimal surface is characterized by having a total curvature equal to zero in every point. This means that for all points on the surface, if the surface is curving with a certain amount in one direction, at the same point the surface will also have to curve with minus the same amount in the normal direction.
If you trap air inside a soap film, and thereby make a bubble, the soap film will no longer be a minimal surface. The film will now enclosure a volume and its total curvature in every point will be larger than zero. The soap film will however still be minimal in the sense that it will present the minimal area with can cover the given volume. You can therefore use the name “minimal construction” for all kinds of soap films. But we do distinguish between minimal surfaces and minimal constructions.
Minimal surfaces and constructions will often be very beautiful shapes. One way to study these shapes is by dipping three-dimensional structures of wire into soap bubbles mixtures. You can for example use a wire formed like a cube.
Minimal surfaces in a wire cube. From top down: A saddle point, a saddle point in the diagonal plane, a diagonal plane.
A complex structure in a cube construction.
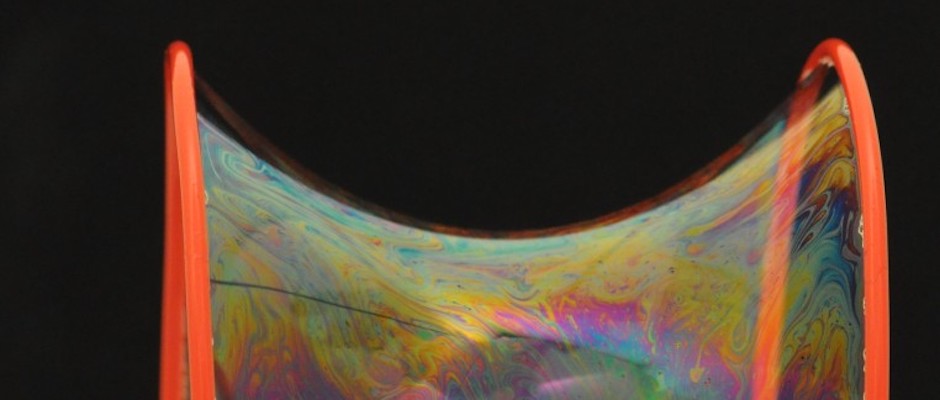
Another beautiful minimal surface is the catenoid. It can be made between two big bubble wands. The properties of a minimal surface can really be seen on the catenoid: That the surface in every point is curving with the same amount in opposite directions.
The mathematical shape “the catenoid” made of a soap film. In every point on its surface its total curvature is zero.
Mathematically the catenoid can be constructed by rotation of the curve for the hyperbolic function, cosh(x).
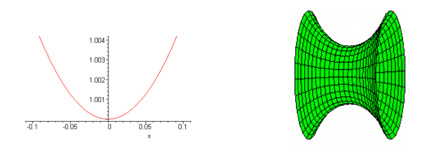
A catenoid (right) is made by rotation of a hyperbolic function (left).
Below, you can see a high speed video of a collapsing catenoid. Notice the small bubble, which is always created in the middle during the collapse of a catenoid.
https://www.youtube.com/watch?v=mziis4pbBOw
A small carrusel inside a bubble.
Her kan du se en film af en almindelig sæbeboblekarrusel
You can build minimal constructions by using two bubble wands (top) or by using a wand and a straw (bottom).