Sæbeboblernes farver
Hvor kommer farverne i sæbebobler fra?
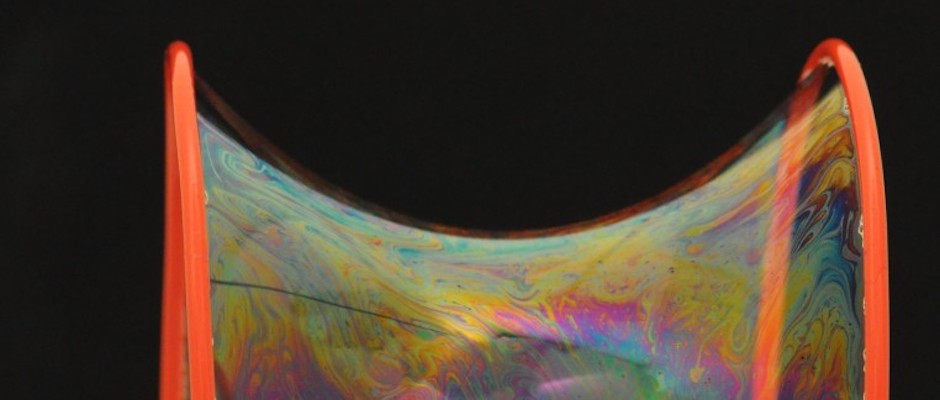
En af de fascinerende ting ved sæbeboblefigurer er at en figur af sæbehinder altid prøver at få så lille en overflade som mulig. For eksempel er en frit svævende boble altid rund og en sæbehinde i et fladt sæbeboblejern er altid flad. I begge tilfælde har sæbehinden den mindst mulige overflade.
Fritsvævende sæbebobler er altid runde fordi sæbeboblen minimerer sit overfladeareal.
I et fladt sæbeboblejern, er sæbehinden altid flad fordi sæbehinden minimerer sit overfladeareal.
At en fritsvævende boble er rund og at en sæbehinde i et fladt sæbeboblejern er flad, er sandt i den matematiske verden. I vores fysiske verden spiller tyngdekraften en vigtig rolle i forhold til de former og farver vi ser i sæbeboblefigurerne. I dette afsnit tager vi udgangspunkt i matematikkens ideelle verden.
Matematisk kalder man figurer der minimerer deres overflade for minimalkonstruktioner. En minimalkonstruktion er kendetegnet ved at det er den konstruktion der har den mindst mulige overflade ud fra nogle givne betingelser. Betingelserne kan for eksempel være den ramme sæbehinden er spændt ud af eller den mængde luft der er indespærret i boblerne. Tyngdekraften er også at betragte som en sådan betingelse. Disse betingelser er faktorer som en boble ikke kan ændre på og derfor bliver nødt til at indordne sig under, hvorimod sæbehindens form ikke er en sådan på forhånd givet betingelse.
Hvis en sæbehinde ikke indeholder nogen bobler, så kaldes den for en minimalflade. Sådan en hinde er kendetegnet ved at den i ethvert punkt på fladen har en krumning på nul. Det vil sige at der for ethvert punkt på fladen gælder at hvis den i én retning buer op set i forhold til tangentplanet i dette punkt, så buer fladen tilsvarende ned i den tværgående retning.
Hvis man fanger luft inde i hinden og altså laver en boble, så er hinden som nævnt ikke længere en minimalflade. Hinden skal nu omslutte et lukket volumen og har derfor en total krumning der er større end nul. Sæbehinderne vil dog stadig være minimale i den forstand at de vil udgøre den mindste overflade som kan omslutte det givne volumen af luft. Man kan derfor lidt løsere kalde alle typer af sæbebobler og sæbehinder for minimalkonstruktioner. Vi skelner altså mellem minimalflader (uden bobler) og de mere generelle minimalkonstruktioner (med eller uden bobler).
Minimalflader og minimalkonstruktioner kan have utrolig flotte former. En måde at studere nogle af disse former på er at tage et ikke fladt sæbeboblejern, dyppe det i sæbevand og betragte de fremkomne former. Benyt for eksempel et kubeformet sæbeboblejern og spræng enkelte dele af sæbehinden i forskellig rækkefølge eller tilføj bobler passende steder. Undervejs kan man observere hvad der sker med den samlede sæbehinde.
Minimalflader i kubeformet sæbeboblejern. Fra oven og ned: Sadelpunkt, sadelpunkt i diagonalsnittet, flad diagonalflade.
En kompleks struktur af bobler i et kubisk gitter.
En anden flot minimalflade er en katenoide. Den dannes ved at lave et ”rør” mellem to runde sæbeboblejern. På kantenoiden kan man rigtigt se hvad der menes med at hvis hinden i én retning buer op set i forhold til tangentplanen i et punkt, så buer den tilsvarende ned i den tværgående retning.
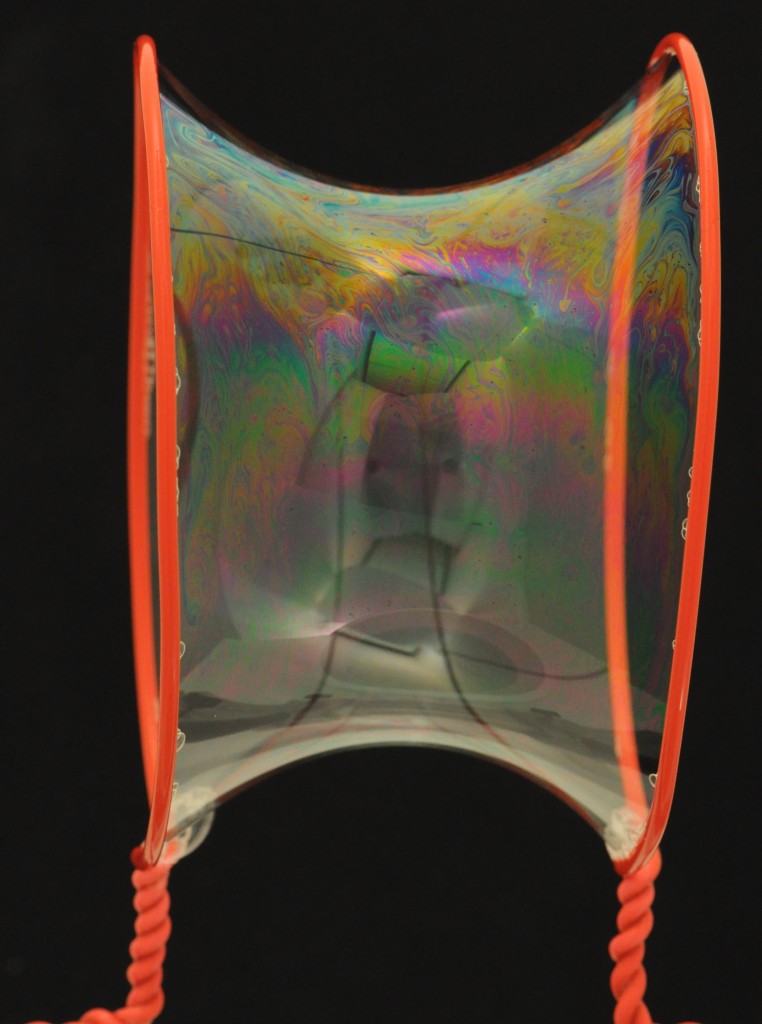
En matematiske figur ”katenoiden” lavet af en sæbehinde. Katenoiden er en minimalflade. Dens samlede krumning i hvert punkt på overfladen er nul.
Matematisk kan en katenoide frembringes ved at rotere en kurve for cosinushyperbolsk omkring en passende linie. Katenoiden er sammen med planet de to eneste omdrejningslegemer der også er minimalflader.
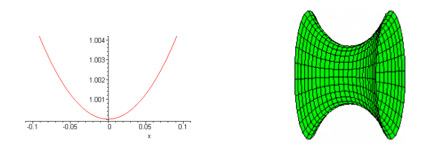
En katenoide (til højre) kan laves ved at rotere en kurve for funktionen cosh(x) (til venstre) omkring en linie
Nedenfor ses en highspeed video af en katenoide, der kollapser. Læg især mærke til den lille boble, der altid skabes i midten af et sådan kollaps.
https://www.youtube.com/watch?v=mziis4pbBOw
En lille karrusel bygget ud af sæbebobler inde i en sæbeboble
Her kan du se en film af en almindelig sæbeboblekarrusel
